【Unity】既存の物理エンジン禁止でシンプルな物理演算を実装する

この記事はUnityゲーム開発者ギルド Advent Calendar 2020最終日の記事です。

adventar.org

こんにちは。 最近はMC Eternalに無限に時間を吸われているnotargsです。

Unityにはとても良くできた物理エンジンの「PhysX」が入っていますが、それを使わずに実装できると便利なときがごくまれににあります。 この記事では、「Position Based Dynamics」というシンプルなアルゴリズムを使って、自前で必要最低限な物理演算を実装する方法について解説します。

Prefabをつくる

まずはPrefabを作り、ランダムに配置していきます。 PrefabにくっつけるScriptをSampleRigidBody、Prefabを生成するScriptをSampleRigidBodyManagerと名付けました。

using UnityEngine;

public sealed class SampleRigidBody : MonoBehaviour
{
}

using System.Collections.Generic;
using UnityEngine;
using Random = Unity.Mathematics.Random;

public sealed class SampleRigidBodyManager : MonoBehaviour
{
    [SerializeField] private SampleRigidBody rigidBodyPrefab;
    
    private readonly List<SampleRigidBody> _rigidBodies = new List<SampleRigidBody>();

    private Random _random;
    
    private void Start()
    {
        _random = new Random(1);
        for (var i = 0; i < 20; ++i)
        {
            var rigidBody = Instantiate(rigidBodyPrefab);
            rigidBody.transform.position = _random.NextFloat3(-1.5f, 1.5f);
            _rigidBodies.Add(rigidBody);
        }
    }
}

SampleRigidBodyはSphereにアタッチしてPrefabにしておきます。

SampleRigidBodyは空のGameObjectにアタッチし、SampleRigidBodyのついたPrefabを設定してSceneに置いておきましょう。

これを実行すると、ランダムにSphereが配置されました。

球同士の衝突判定を行う

続いて、球同士の衝突判定を行い、衝突していたら反発させる処理を書きます。

全ての球について、他の全ての球に対して衝突判定を行うと、球の数 * 球の数 O(n^2) の処理が必要になり、球の数が増えるほど、指数関数的に重くなってしまいます。 そのため、一般的には、次の２つのフェーズに分けて衝突判定を行います。 - ブロードフェーズ: シンプルな形状で大まかな衝突判定を行って枝刈りを行うフェーズ - ナローフェーズ: 詳細な形状に合わせて正確に衝突判定を行うフェーズ

が、ここではめんどくさいためブロードフェーズは省略します。 興味がある人はブロードフェーズ スイープ＆プルーン Bounding Volume Hierarchyなどのキーワードで検索してみてください。

球の半径を0.5としたとき、球同士の距離が1以下なら衝突しているため、それを用いて衝突を判定します。

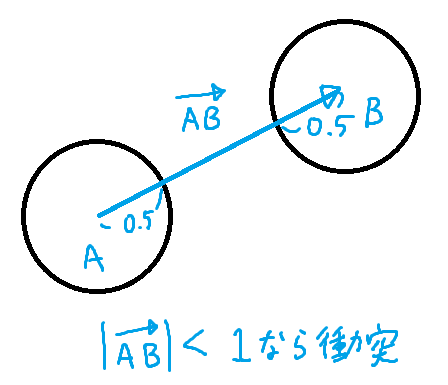
衝突していたら、球同士がちょうどぶつからない場所までそれぞれの位置をずらしてあげます。

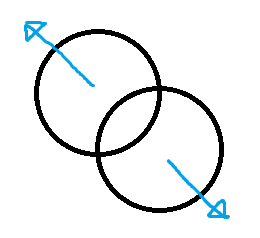
物理挙動はUpdateで計算を行うと不安定になってしまいがちなので、FixedUpdate内で行います。

using System.Collections.Generic;
using UnityEngine;
using Random = Unity.Mathematics.Random;

public sealed class SampleRigidBodyManager : MonoBehaviour
{
    [SerializeField] private SampleRigidBody rigidBodyPrefab;
    
    private readonly List<SampleRigidBody> _rigidBodies = new List<SampleRigidBody>();

    private Random _random;
    
    private void Start()
    {
        _random = new Random(1);
        for (var i = 0; i < 20; ++i)
        {
            var rigidBody = Instantiate(rigidBodyPrefab);
            rigidBody.transform.position = _random.NextFloat3(-1.5f, 1.5f);
            _rigidBodies.Add(rigidBody);
        }
    }

    private void FixedUpdate()
    {
        for (var i = 0; i < _rigidBodies.Count - 1; ++i)
        {
            for (var j = i; j < _rigidBodies.Count; ++j)
            {
                var rigidBody1 = _rigidBodies[i];
                var rigidBody2 = _rigidBodies[j];
                if (rigidBody1 == rigidBody2)
                {
                    continue;
                }
                
                var a = rigidBody1.transform.position;
                var b = rigidBody2.transform.position;
                
                var ab = b - a;
                
                var abMagnitude = ab.magnitude;
                var abDirection = ab.normalized;
                if (abDirection == Vector3.zero) abDirection = Vector3.up;
                
                if (abMagnitude < 1)
                {
                    a -= (1 - abMagnitude) * abDirection / 2;
                    b += (1 - abMagnitude ) * abDirection / 2;
                }
                
                rigidBody1.transform.position = a;
                rigidBody2.transform.position = b;
            }
        }
    }
}

球同士が衝突し、反発するようになりました。

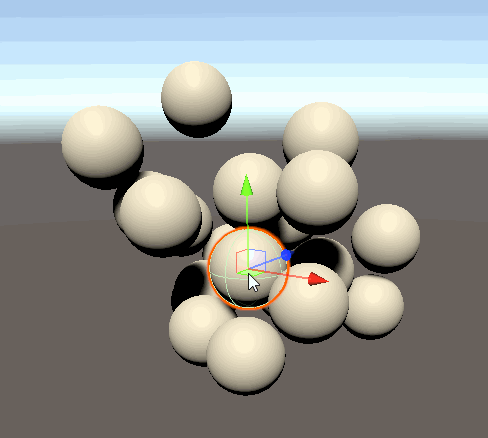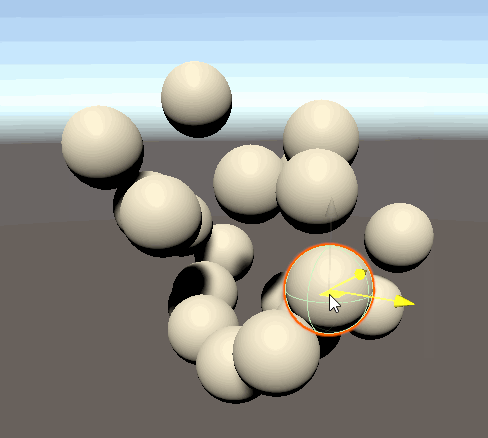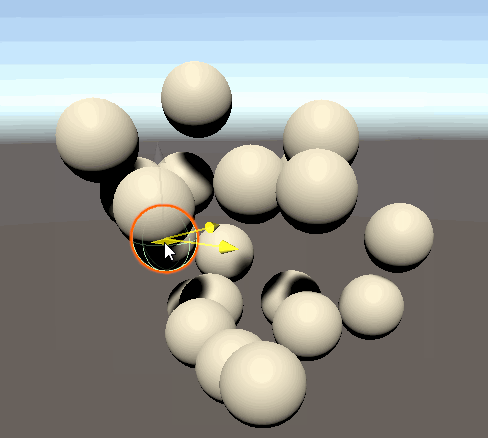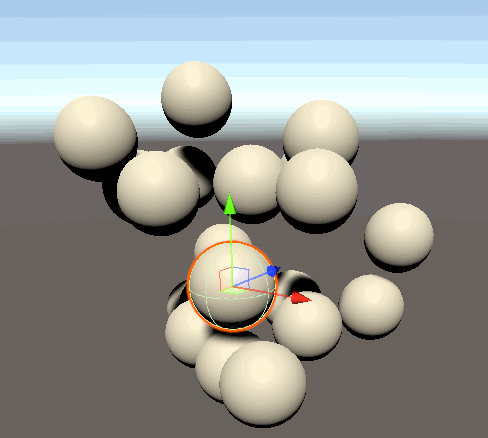
壁を作る

球がどこまでも飛んでいってしまわないように、壁を作ります。 とはいってもやることは座標を制限するだけなので、とても簡単です。

a = math.clamp(a, -2, 2);
b = math.clamp(b, -2, 2);

この2行をFixedUpdateの最後に追記してあげましょう。

using System.Collections.Generic;
using Unity.Mathematics;
using UnityEngine;
using Random = Unity.Mathematics.Random;

public sealed class SampleRigidBodyManager : MonoBehaviour
{
    [SerializeField] private SampleRigidBody rigidBodyPrefab;
    
    private readonly List<SampleRigidBody> _rigidBodies = new List<SampleRigidBody>();

    private Random _random;
    
    private void Start()
    {
        _random = new Random(1);
        for (var i = 0; i < 20; ++i)
        {
            var rigidBody = Instantiate(rigidBodyPrefab);
            rigidBody.transform.position = _random.NextFloat3(-1.5f, 1.5f);
            _rigidBodies.Add(rigidBody);
        }
    }

    private void FixedUpdate()
    {
        for (var i = 0; i < _rigidBodies.Count - 1; ++i)
        {
            for (var j = i; j < _rigidBodies.Count; ++j)
            {
                var rigidBody1 = _rigidBodies[i];
                var rigidBody2 = _rigidBodies[j];
                if (rigidBody1 == rigidBody2)
                {
                    continue;
                }
                
                var a = rigidBody1.transform.position;
                var b = rigidBody2.transform.position;
                
                var ab = b - a;
                
                var abMagnitude = ab.magnitude;
                var abDirection = ab.normalized;
                if (abDirection == Vector3.zero) abDirection = Vector3.up;
                
                if (abMagnitude < 1)
                {
                    a -= (1 - abMagnitude) * abDirection / 2;
                    b += (1 - abMagnitude ) * abDirection / 2;
                }

                a = math.clamp(a, -2, 2);
                b = math.clamp(b, -2, 2);
                
                rigidBody1.transform.position = a;
                rigidBody2.transform.position = b;
            }
        }
    }
}

位置の制限が実装できました！ Gizmoを使って強制的に座標を上書きしたためにぷるぷるしていますが、ここでは気にしないこととします。

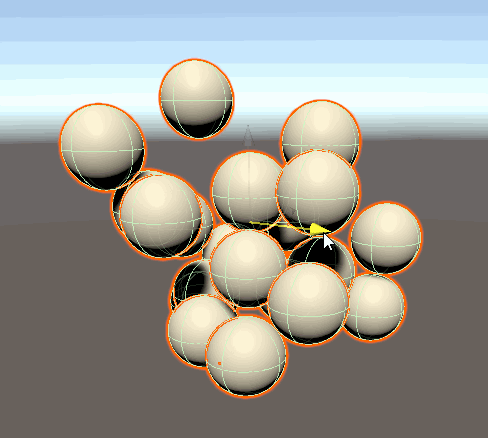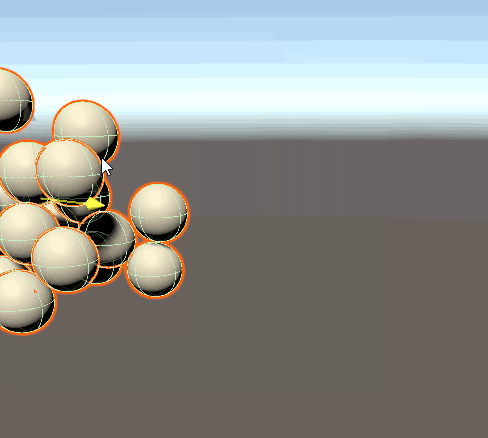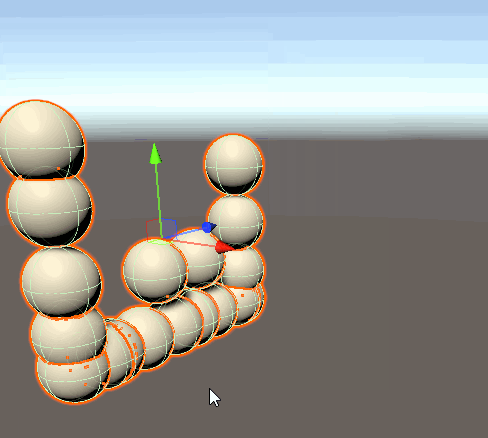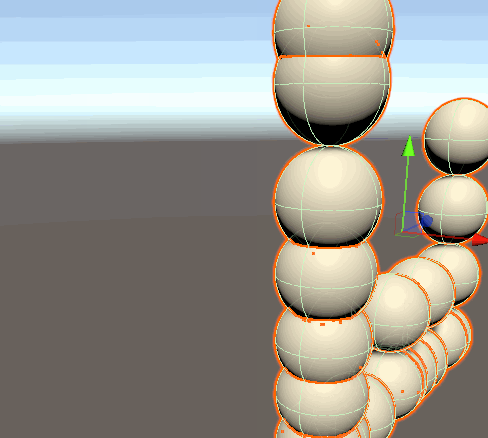
速度の概念を作る

続いて、「速度」を実装していきます。 SampleRigidBody.csに「1フレーム前の自身の位置」を保存しておき、速度が必要になったタイミングで都度計算するアプローチで実装していきます。 「速度」をそのまま各RigidBodyに持たせることもできますが、反発したときに速度の再計算などが必要になってくるため、より楽な方を選びました。

using UnityEngine;

public sealed class SampleRigidBody : MonoBehaviour
{
    public Vector3 PrevPosition { get; set; }
}

SampleRigidBodyManager.csのFixedUpdate内に、速度の計算、位置の更新、前の位置の更新処理を追記します。

foreach (var rigidbody in _rigidBodies)
{
    var position = rigidbody.transform.position;
    var velocity = (position - rigidbody.PrevPosition) / Time.deltaTime;

    rigidbody.PrevPosition = position;
    position += velocity * Time.deltaTime;
    
    rigidbody.transform.position = position;
}

SampleRigidBodyManager.csの全文は次のようになりました。

using System.Collections.Generic;
using Unity.Mathematics;
using UnityEngine;
using Random = Unity.Mathematics.Random;

public sealed class SampleRigidBodyManager : MonoBehaviour
{
    [SerializeField] private SampleRigidBody rigidBodyPrefab;
    
    private readonly List<SampleRigidBody> _rigidBodies = new List<SampleRigidBody>();

    private Random _random;
    
    private void Start()
    {
        _random = new Random(1);
        for (var i = 0; i < 20; ++i)
        {
            var rigidBody = Instantiate(rigidBodyPrefab);
            rigidBody.transform.position = _random.NextFloat3(-1.5f, 1.5f);
            _rigidBodies.Add(rigidBody);
        }
    }
    
    private void FixedUpdate()
    {
        foreach (var rigidbody in _rigidBodies)
        {
            var position = rigidbody.transform.position;
            var velocity = (position - rigidbody.PrevPosition) / Time.deltaTime;

            rigidbody.PrevPosition = position;
            position += velocity * Time.deltaTime;
            
            rigidbody.transform.position = position;
        }

        for (var i = 0; i < _rigidBodies.Count - 1; ++i)
        {
            for (var j = i; j < _rigidBodies.Count; ++j)
            {
                var rigidBody1 = _rigidBodies[i];
                var rigidBody2 = _rigidBodies[j];
                if (rigidBody1 == rigidBody2)
                {
                    continue;
                }
                
                var a = rigidBody1.transform.position;
                var b = rigidBody2.transform.position;
                
                var ab = b - a;
                
                var abMagnitude = ab.magnitude;
                var abDirection = ab.normalized;
                if (abDirection == Vector3.zero) abDirection = Vector3.up;
                
                if (abMagnitude < 1)
                {
                    a -= (1 - abMagnitude) * abDirection / 2;
                    b += (1 - abMagnitude ) * abDirection / 2;
                }

                a = math.clamp(a, -2, 2);
                b = math.clamp(b, -2, 2);
                
                rigidBody1.transform.position = a;
                rigidBody2.transform.position = b;
            }
        }
    }
}

これを動かしてみると、フレームをまたいで速度が維持されていることがわかります。

だいぶ物理っぽくなってきました。

重力を加える

velocity += Physics.gravity * Time.deltaTime;

の1行を加えることで、重力を実装してみます。

using System.Collections.Generic;
using Unity.Mathematics;
using UnityEngine;
using Random = Unity.Mathematics.Random;

public sealed class SampleRigidBodyManager : MonoBehaviour
{
    [SerializeField] private SampleRigidBody rigidBodyPrefab;
    
    private readonly List<SampleRigidBody> _rigidBodies = new List<SampleRigidBody>();

    private Random _random;
    
    private void Start()
    {
        _random = new Random(1);
        for (var i = 0; i < 20; ++i)
        {
            var rigidBody = Instantiate(rigidBodyPrefab);
            rigidBody.transform.position = _random.NextFloat3(-1.5f, 1.5f);
            _rigidBodies.Add(rigidBody);
        }
    }

    private void FixedUpdate()
    {
        foreach (var rigidbody in _rigidBodies)
        {
            var position = rigidbody.transform.position;
            var velocity = (position - rigidbody.PrevPosition) / Time.deltaTime;

            velocity += Physics.gravity * Time.deltaTime;

            rigidbody.PrevPosition = position;
            position += velocity * Time.deltaTime;
            
            rigidbody.transform.position = position;
        }

        for (var i = 0; i < _rigidBodies.Count - 1; ++i)
        {
            for (var j = i; j < _rigidBodies.Count; ++j)
            {
                var rigidBody1 = _rigidBodies[i];
                var rigidBody2 = _rigidBodies[j];
                if (rigidBody1 == rigidBody2)
                {
                    continue;
                }
                
                var a = rigidBody1.transform.position;
                var b = rigidBody2.transform.position;
                
                var ab = b - a;
                
                var abMagnitude = ab.magnitude;
                var abDirection = ab.normalized;
                if (abDirection == Vector3.zero) abDirection = Vector3.up;
                
                if (abMagnitude < 1)
                {
                    a -= (1 - abMagnitude) * abDirection / 2;
                    b += (1 - abMagnitude ) * abDirection / 2;
                }

                a = math.clamp(a, -2, 2);
                b = math.clamp(b, -2, 2);
                
                rigidBody1.transform.position = a;
                rigidBody2.transform.position = b;
            }
        }
    }
}

物体が重力に沿って落下するようになりました。

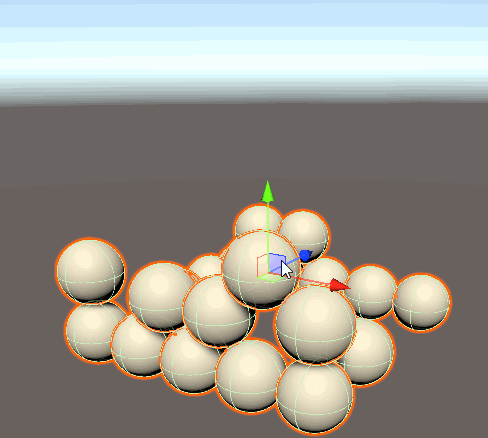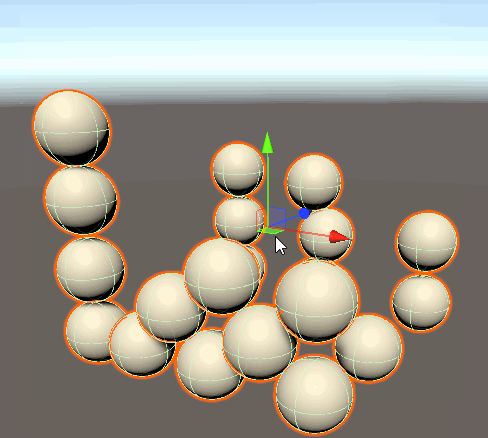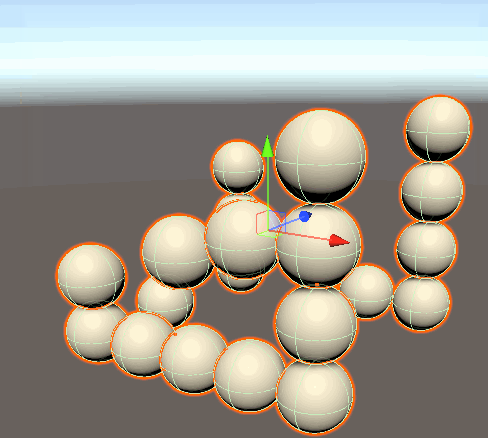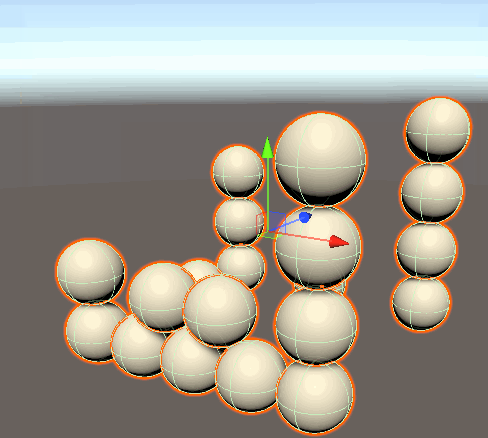
台パンを実装する

せっかくなので、台を揺らすようなイメージで、物体を跳ねさせる仕組みを実装してみましょう。 SampleRigidBodyManager.csに、「Zキーが押されたときに球をランダムな方向に移動させる」処理を書きこみます。

private void Update()
{
    if (Input.GetKeyDown(KeyCode.Z))
    {
        foreach (var rigidbody in _rigidBodies)
        {
            rigidbody.transform.position += (Vector3)_random.NextFloat3Direction() * 0.1f;
        }
    }
}

全文はこのようになりました。

using System.Collections.Generic;
using Unity.Mathematics;
using UnityEngine;
using Random = Unity.Mathematics.Random;

public sealed class SampleRigidBodyManager : MonoBehaviour
{
    [SerializeField] private SampleRigidBody rigidBodyPrefab;
    
    private readonly List<SampleRigidBody> _rigidBodies = new List<SampleRigidBody>();

    private Random _random;
    
    private void Start()
    {
        _random = new Random(1);
        for (var i = 0; i < 20; ++i)
        {
            var rigidBody = Instantiate(rigidBodyPrefab);
            rigidBody.transform.position = _random.NextFloat3(-1.5f, 1.5f);
            _rigidBodies.Add(rigidBody);
        }
    }

private void Update()
{
    if (Input.GetKeyDown(KeyCode.Z))
    {
        foreach (var rigidbody in _rigidBodies)
        {
            rigidbody.transform.position += (Vector3)_random.NextFloat3Direction() * 0.1f;
        }
    }
}

    private void FixedUpdate()
    {
        foreach (var rigidbody in _rigidBodies)
        {
            var position = rigidbody.transform.position;
            var velocity = (position - rigidbody.PrevPosition) / Time.deltaTime;

            velocity += Physics.gravity * Time.deltaTime;

            rigidbody.PrevPosition = position;
            position += velocity * Time.deltaTime;
            
            rigidbody.transform.position = position;
        }

        for (var i = 0; i < _rigidBodies.Count - 1; ++i)
        {
            for (var j = i; j < _rigidBodies.Count; ++j)
            {
                var rigidBody1 = _rigidBodies[i];
                var rigidBody2 = _rigidBodies[j];
                if (rigidBody1 == rigidBody2)
                {
                    continue;
                }
                
                var a = rigidBody1.transform.position;
                var b = rigidBody2.transform.position;
                
                var ab = b - a;
                
                var abMagnitude = ab.magnitude;
                var abDirection = ab.normalized;
                if (abDirection == Vector3.zero) abDirection = Vector3.up;
                
                if (abMagnitude < 1)
                {
                    a -= (1 - abMagnitude) * abDirection / 2;
                    b += (1 - abMagnitude ) * abDirection / 2;
                }

                a = math.clamp(a, -2, 2);
                b = math.clamp(b, -2, 2);
                
                rigidBody1.transform.position = a;
                rigidBody2.transform.position = b;
            }
        }
    }
}

まとめ

ここまで、シンプルな仕組みで物理エンジンのようなものを自前実装してみました。 DynamicBoneやVRMSpringBone、UnityちゃんSpringBoneなどの「揺れもの」はこの仕組みベースに、さらに次のような要素を組み込むことで実現されています。

• 物体同士を紐のようなものでつなげる
• 繋がっている物体同士の距離を一定距離に制限
• 繋がっている物体が一定の位置関係を保つように力を加える

ここまで解説した内容がしっかりと理解できていれば、これらのソースコードもそれほど苦戦することなく読み解くことができると思います。 ぜひともチャレンジしてみてください。

【Unity】PostProcessingStackのBloomで「特定の物体だけ」を光らせる方法

この記事はUnityアドベントカレンダー2020、2日目の記事です。 qiita.com

Unityについての質問で、次のような質問をよく見かけます。

「特定の物体にだけポストエフェクトを掛けることはできますか？」

これは一応可能ですが、UnityのレイヤーはPhotoshopのレイヤーとは全くの別物で、めちゃくちゃめんどくさいため初心者にはおすすめしません。

どうしてそんなことがしたくなったのかを聞いてみると、「特定の物体だけをBloomで光らせたい」という目的が出てくることが多いです。 これは結構簡単にできるので、やり方をまとめてみました！

そもそもBloomってなんだ？

現実世界のカメラや人間の目は、レンズを通して入ってきた光をセンサーで検知して「色」を判別します。

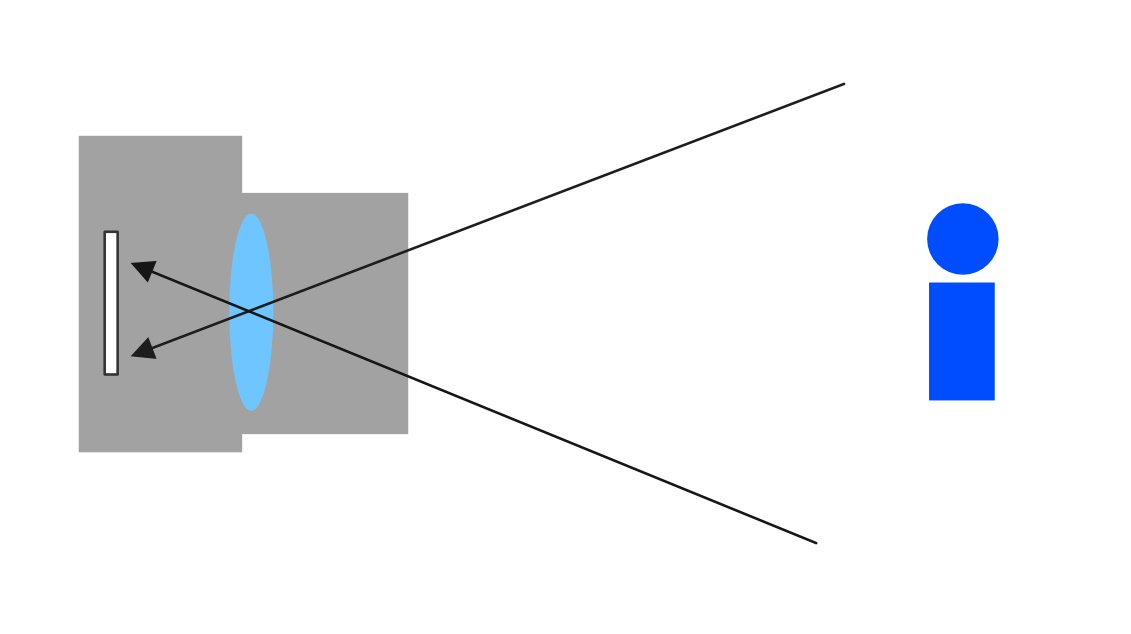
ですが、この光は全てがまっすぐ目に届くわけではありません。

ごくわずかな光がカメラの内部構造・レンズ・空気など（！）によって屈折、乱反射し、減衰・拡散してから光センサーに届きます。 （ちなみに、「フォグ」も空気による散乱をシミュレーションするための効果です。）

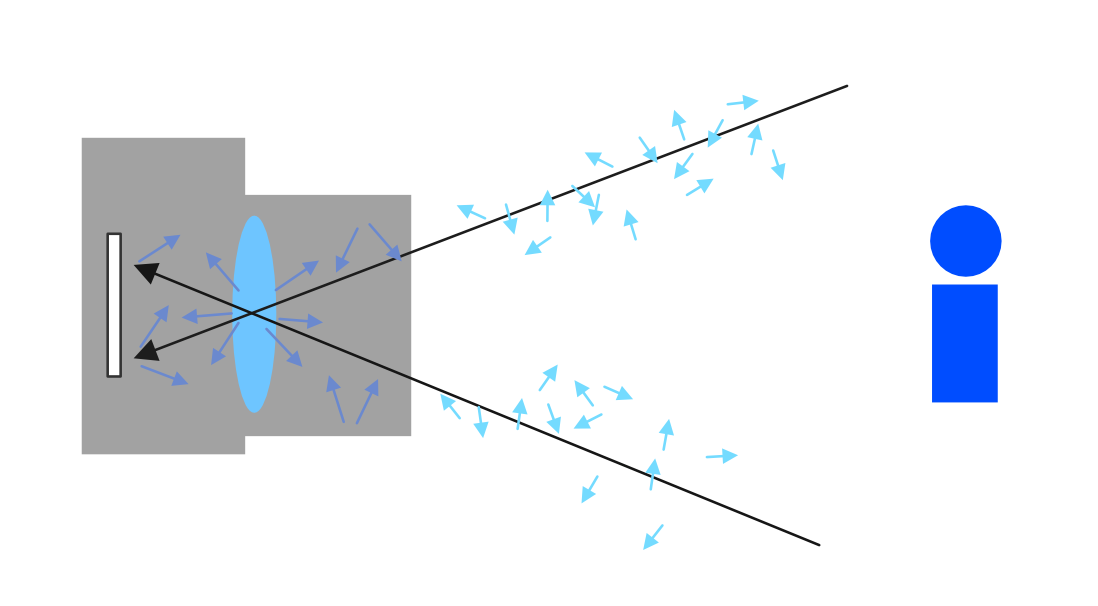
これを真面目にシミュレーションするととても重いので、真面目に計算せず、それっぽく表現するためのエフェクトがBloomです。

Bloomは、厳密に光をシミュレーションしたものではありません。

「物体を光らせる」ためのエフェクトではなく、あくまで「光っているように見せる」エフェクトという点に注意しましょう。

Bloomの仕組み

Bloomは、基本的に次の3つのステップで実装されています。

まず、元画像の色彩を調整し、一定より明るい部分だけを取り出します。

元画像

明るい部分だけ取り出したもの

続いて、明るい部分だけを取り出したものをぼかします。 処理を高速にするため、一旦縮小を掛けてからぼかすこともあります。

ぼかしたもの

最後に、ぼかした画像の色を、元画像の画像の色にそれぞれ足し合わせます。

ぼかしたものを元画像に加算合成したもの

PostProcessingStackのBloomのパラメーターを見てみる

PostProcessingStackのBloomのパラメーターを見てみましょう。

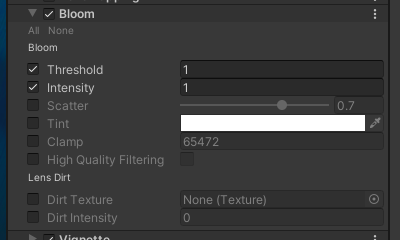
ここで重要な値は、次の2つのパラメーターです。

• Threshold
  • いくつ以上の明るさの箇所を取り出すか？
• Scatter
  • ぼかしの大きさ

「Threshold」は、基本的には「黒」を0、「白」を1としたときの明るさで表されます。 パッと見0～1の範囲で入力すればいいように見えますが、ここで、Thresholdに1以上の値が入力できることに気づけます。

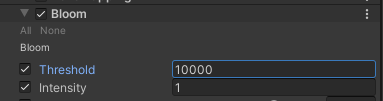
HDRについて

Unityには「HDR(High Dynamic Range)」という機能があります。 「HDR」は、白(0)～黒(1)の範囲を超えた、「とても明るい色」を表現するための機能です。 逆に、白(0)～黒(1)の範囲の中の色のみを使っている状態を「LDR(Low Dynamic Range)」と言います。

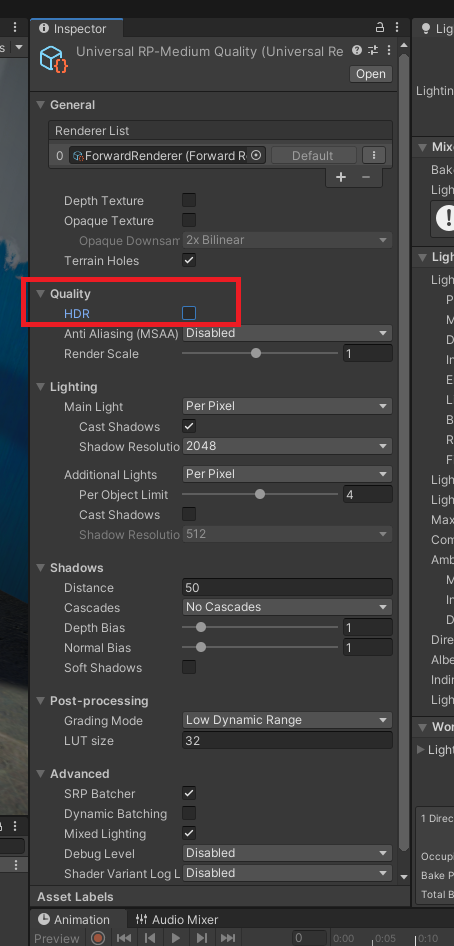
HDRはデフォルトでは無効になっており、設定から有効化する必要があります。 ここでは一例として、UniversalRenderPipelineでのHDRの有効化方法を紹介します。

URPでは、Renderer AssetのQualityセクション内に「HDR」のチェックボックスがあります。

マテリアルのEmissionについて

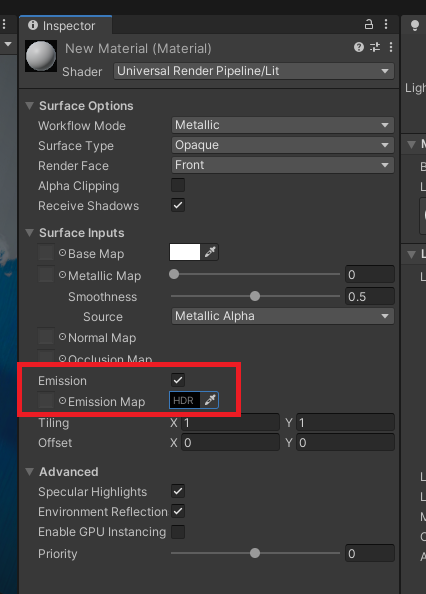
Unityのマテリアルには、「Emission」というパラメーターがあります。

通常の物体は入ってきた光を減衰・拡散させて反射させます。 入ってきた光より多い量の光が出ていくことはありません。

Emissionはそれに加えて、「物体自身が放出している色」を設定するパラメーターです。 Emissionの設定された物体は、「発光している物体」とみなせます。

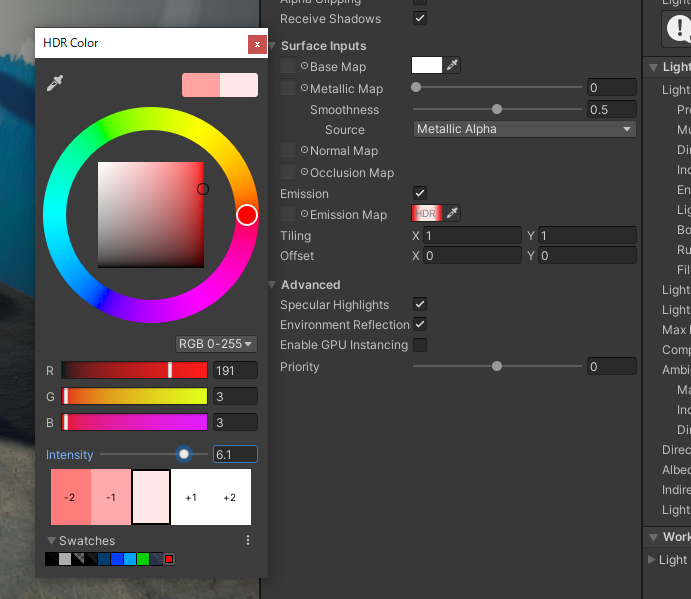
EmissionのカラーピッカーはHDRに対応しており、Intencityを上げることで、白(1)より明るい色を設定することができます。 白より明るい色が設定されている場合、インスペクタ上での色の表示も少し特殊な見た目になります。

で、どうすればいいの？

以上を踏まえて、Bloomを利用して「特定の物体だけを光らせる」方法は次の通りになります。

• RenderPipelineの設定からHDRを有効化する
• Emissionを1以上の値に設定したマテリアルを作成し、オブジェクトにアタッチする
• Bloomの設定から、Thresholdを1以上、Emissionで設定した明るさ以下の値に設定する

これらの作業をすることで、特定の物体に対してのみ、しっかりBloomがかかった絵を作ることができます。

まずBloomの事は考えずに「この物体は太陽光の2倍の明るさだ」といった基準でEmissionを決めてあげ、あとからBloomを調整してあげるのがおすすめです。

うおっまぶしっ

それでは、よきBloomライフを！

【Unity】PackageManagerからExtenject、UniRx、UniTaskをお手軽に導入する

Unity2019.3から、PackageManagerにて相対パスでgithubにあるPackageが導入できるようになりました。 備忘録として、現行バージョン（2020/7/25時点）のExtenject、UniRx、UniTaskを導入する方法についてメモっておきます。

やりかた

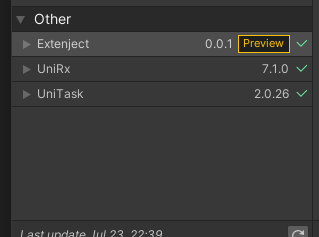
• Packages/manifest.json内に以下を追記し、Unityのウィンドウをアクティブにします。

"com.svermeulen.extenject": "https://github.com/svermeulen/Extenject.git?path=UnityProject/Assets/Plugins/Zenject",
"com.neuecc.unirx": "https://github.com/neuecc/UniRx.git?path=Assets/Plugins/UniRx/Scripts",
"com.cysharp.unitask": "https://github.com/Cysharp/UniTask.git?path=src/UniTask/Assets/Plugins/UniTask"

無事導入できました！

つぶやきGLSLで今すぐ使えるシェーダーminifyテクニック11選！

最近、1ツイート(280文字)内にシェーダーをおさめる つぶやきGLSL というものが流行っています。

一見「もうこれ以上詰められないよ～」となってしまっても、よくよく探すと意外なところを削れることがあったります。

この記事では、自分が使っている、つぶやきGLSLで文字を詰めるためのテクニックをチートシートとしてまとめてみました。

つぶやきGLSLの作例

#つぶやきGLSL
void main(){vec3 p;for(int i=0;i<32;++i)p+=vec3((gl_FragCoord.xy*2.-r)/r.y,1)*(length(cos(p))-length(sin(t/.1+p/.2))*.6*s)*.5;gl_FragColor=vec4(5./p.z*s);}

vec2 mainSound(float t){int i=int(t*=1e3);return vec2(((-(i>>8)%8)*((i>>3&i)|((i>>5)&(i<<5))))&255)/127.-1.;} pic.twitter.com/z4Zt5Vbj3O

— notargs (@notargs) 2020年4月17日

#つぶやきGLSL
void main(){vec2 p=(gl_FragCoord.xy*2.-r)/r.y;o=vec4(min(min(min(abs(max(-max(.5-length(p),(p.x=abs(p.x))-p.y*.5),length(p)-.8)),max(min(abs(p.y),abs(abs(p.y)-p.x*.3)),abs(p.x-.9)-.2)),length(p-vec2(.15,.3))),max(abs(length(p-vec2(.05,.2))-.05),p.y-.18)))/.03;} pic.twitter.com/EYL7yLuqkJ

— notargs (@notargs) 2020年4月18日

#つぶやきGLSL
float f(vec3 p){p.z-=t*10.;float a=p.z*.1;p.xy *= mat2(cos(a),sin(a),-sin(a),cos(a));return .1-length(cos(p.xy)+sin(p.yz));}void main(){vec3 d=.5-vec3(gl_FragCoord.xy,1)/r.y,p;for(int i=0;i<32;i++)p+=f(p)*d;gl_FragColor.xyz=(sin(p)+vec3(2,5,9))/length(p);} pic.twitter.com/mNwavsLDRN

— notargs (@notargs) 2020年4月15日

つぶやきGLSLの参考記事

webgl.souhonzan.org

今回使うエディタ

この記事では、twigl.appを前提として解説します。 twigl.app

基本的なテクニック

twigl.appのregulationはclassicではなくgeeker(300 es)を使う

twigl.appには、いくつかのregulationが存在します。

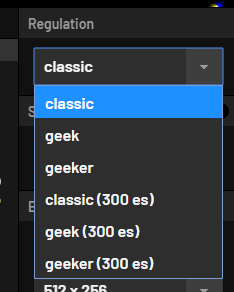
デフォルトで選ばれているのは classic ですが、 classic はマゾ向けです。強いこだわりがなければ geeker(300 es)を選びましょう。

geekerが選ばれている作品もよく見ますが、geeker(300 es)にすることでgl_FragColor=vec4(p.xxy,1);をo=vec4(p.xxy,1);と省略できるため、300 esのほうがおすすめです。

各レギュレーションの比較

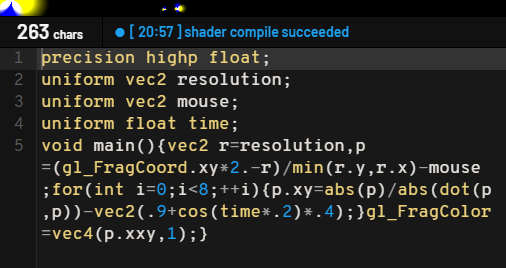
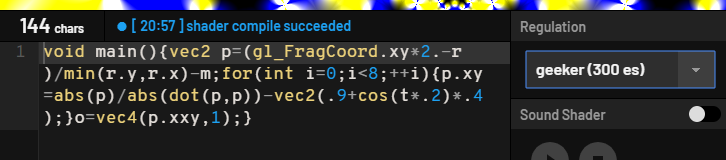
数値リテラルを短く書く

GLSLでは、0.2fを.2、8.0fを8.のように、小数点を挟んだ0とfは省略できます。

また、指数表記を使うことで、100000を1e5のように節約して書くこともできます。

ベクトルの定義を短く書く

GLSLではベクトルの初期化時に、

vec4 a=vec4(0,0,0,0);

のように、int型を代入できます。

更に、全て同じ値であれば、

vec4 a=vec4(0);

のように1つの要素を用いて初期化もできます。

geeker(300 es)のサンプルコードをminifyしてみる

geeker(300 es)を選んだときに、最初から入っているサンプルコードを小さくしてみます。

void main(){vec2 p=(gl_FragCoord.xy*2.-r)/min(r.y,r.x)-m;for(int i=0;i<8;++i){p.xy=abs(p)/abs(dot(p,p))-vec2(.9+cos(t*.2)*.4);}o=vec4(p.xxy,1);}

座標を計算する

twigl.appのデフォルトでは次のような座標を計算するスクリプトが入っています。

vec2 p=(gl_FragCoord.xy*2.-r)/min(r.y,r.x)-m;

これもちらほら表現によっては不要なところがあるので、削ってしまいましょう。

まず、マウス位置はいらないので削ってしまいます。

vec2 p=(gl_FragCoord.xy*2.-r)/min(r.y,r.x);

大抵の場合縦幅のほうが横幅より小さいので、常に縦幅で割るように変更します。

vec2 p=(gl_FragCoord.xy*2.-r)/r.y;

これだけで10文字削れました。

また、少しズルいですが、rを決め打ちしてしまうことで、より文字数を減らすこともできます。

vec2 p=gl_FragCoord.xy/1e2-3.;

暗黙的な型変換を活用する

GLSLには、ベクトルとスカラーの足し算を行ったときなど、自動でスカラーをベクトルと見なして演算してくれる機能があります。

例えば、twigl.appのサンプルにあるこの式は、

p.xy=abs(p)/abs(dot(p,p))-vec2(.9+cos(t*.2)*.4);

このように省略して書けます。

p.xy=abs(p)/abs(dot(p,p))-(.9+cos(t*.2)*.4);

邪魔なvec2のconstructがなくなったので、マイナスを展開するとかっこが外せて2文字節約できます。

p.xy=abs(p)/abs(dot(p,p))-.9-cos(t*.2)*.4;

左辺のpも右辺も同じvec2なので、ついでに不要な.xyも消してしまいましょう。

p=abs(p)/abs(dot(p,p))-.9-cos(t*.2)*.4;

同じ命令は出来る限りまとめる

|a/b| = |a|/|b|なので、

abs(p)/abs(dot(p,p))

は

abs(p/dot(p,p))

のように書けます。

他にも、(ab+ac)=a(b+c)など、数式の変形を用いて順序を変えることでより文字数を減らせる局面があるので、ぜひ探してみましょう。

for文のカッコを省略する

for文のカッコ{}は、forの内部が1つの式であれば省略できます。

for(int i=0;i<8;++i){p=abs(p/dot(p,p))-.9-cos(t*.2)*.4;}

↓

for(int i=0;i<8;++i)p=abs(p/dot(p,p))-.9-cos(t*.2)*.4;

for文の中身に複数の式があるときも、セミコロン;の代わりにカンマ,を使うことで、複数の式を結合して一つの式にできます。

for(int i=0;i<8;++i){p=abs(p/dot(p,p));p-=.9-cos(t*.2)*.4;}

↓

for(int i=0;i<8;++i)p=abs(p/dot(p,p)),p-=.9-cos(t*.2)*.4;

出力のα値は何でも良いことを利用する

twigl.appの現バージョンでは、出力の4つめの値（本来は透明度を示す値）はどんな値でも正しく表示されるようになっています。 適当な値を入れて問題ないため、

o=vec4(p.xxy,1);

を

o=p.xxyy;

のように省略できます。

出力用の変数oを利用する

geeker(300 es)の出力用変数であるvec4型のoは、main関数内で何度でも再代入できます。 あるものは使ってしまいましょう。

void main(){
    vec2 p=gl_FragCoord.xy/1e2-3.;
    for(int i=0;i<8;++i)p=abs(p/dot(p,p))-.9-cos(t*.2)*.4;
    o=p.xxyy;
}

↓

void main(){
    o=gl_FragCoord.xxyy/1e2-3.;
    for(int i=0;i<8;++i)o=abs(o/dot(o.xz,o.xz))-.9-cos(t*.2)*.4;
}

pの定義を削り、oをp代わりに使うように変更しました。

元のコードと見比べてみる

元のコードと見比べてみます。

void main(){vec2 p=(gl_FragCoord.xy*2.-r)/min(r.y,r.x)-m;for(int i=0;i<8;++i){p.xy=abs(p)/abs(dot(p,p))-vec2(.9+cos(t*.2)*.4);}o=vec4(p.xxy,1);}

↓

void main(){o=gl_FragCoord.xxyy/1e2-3.;for(int i=0;i<8;++i)o=abs(o/dot(o.xz,o.xz))-.9-cos(t*.2)*.4;}

144chars→100charsと、なかなか短くできたのではないでしょうか。

その他応用的なテクニック

ここからは、その他の応用的なテクニックについて解説します。

回転行列を短く定義する

glslでは、回転を表現するために、

v = mat2(cos(a), -sin(a), sin(a), cos(a)) * v;

のような回転行列がよく使われます。

これをより短く定義できないか考えてみましょう。

cos(θ) = sin(θ + π/2) なので、sin/cosを統一して次のように書くことができます。

#define PI 3.1415926535
v = mat2(cos(a+vec4(0,-PI/2.,PI/2,0))) * v;

更に、PIの定義が長すぎるため、ここをより短く定義できないかを考えます。 cosは2πで一周するため、cos(-π/2)、cos(π/2)に近い値となる、整数の数値を探してみます。

sin(π/2) = 1
sin(8) = 0.98935824662

sin(-π/2) = -1
sin(5) = -0.95892427466

どうやら8と5が近そうです。

v = mat2(cos(a+vec4(0,8,5,0))) * v;

かなり短くなりました！

変数の代入を式として使う

a = vec3(1);
a += a;
a *= a;

のような代入は、実はvec3を返す式として扱うことができます。 そのまま変数に代入できるため、

a*=a+=(a=vec3(1));

のようにminifyできます。

まとめ

つぶやきGLSLはお手軽に始めることができ、なおかつコードゴルフとアートが密接に結びついた、とても楽しい娯楽だと思います。 ぜひGWをtwigl.appで過ごしましょう！